The intuition behind Frequentist linear regression, Bayesian linear regression and Gaussian Processes
A consequence of believing in the consilience of knowledge is that we believe all knowledge is connected. We can make analogies amongst pieces of knowledge that can help us understand them.
One thing I like to do with analogies is to grasp some intuition behind probabilistic models, which I hope is useful for concepts which are inherently hard to undersatnd such as Bayesianism, especially if you are accustomed to frequentist statistical modelling.
The following hopefully helps you distinguish frequentist linear regression, from Bayesian linear regression, and Gaussian processes. It is worth noting that this article is NOT technical in terms of probability theory, and I recommend going through the Recommended Reading before continuing.
Frequentist linear regression:
Imagine that on a sheet of paper with some dots drawn on them, you ask yourself how can you place a ruler to fit those dots. You only place a unique ruler. This ruler can be of any shape, whether it’s a grader, straight or triangular ruler.
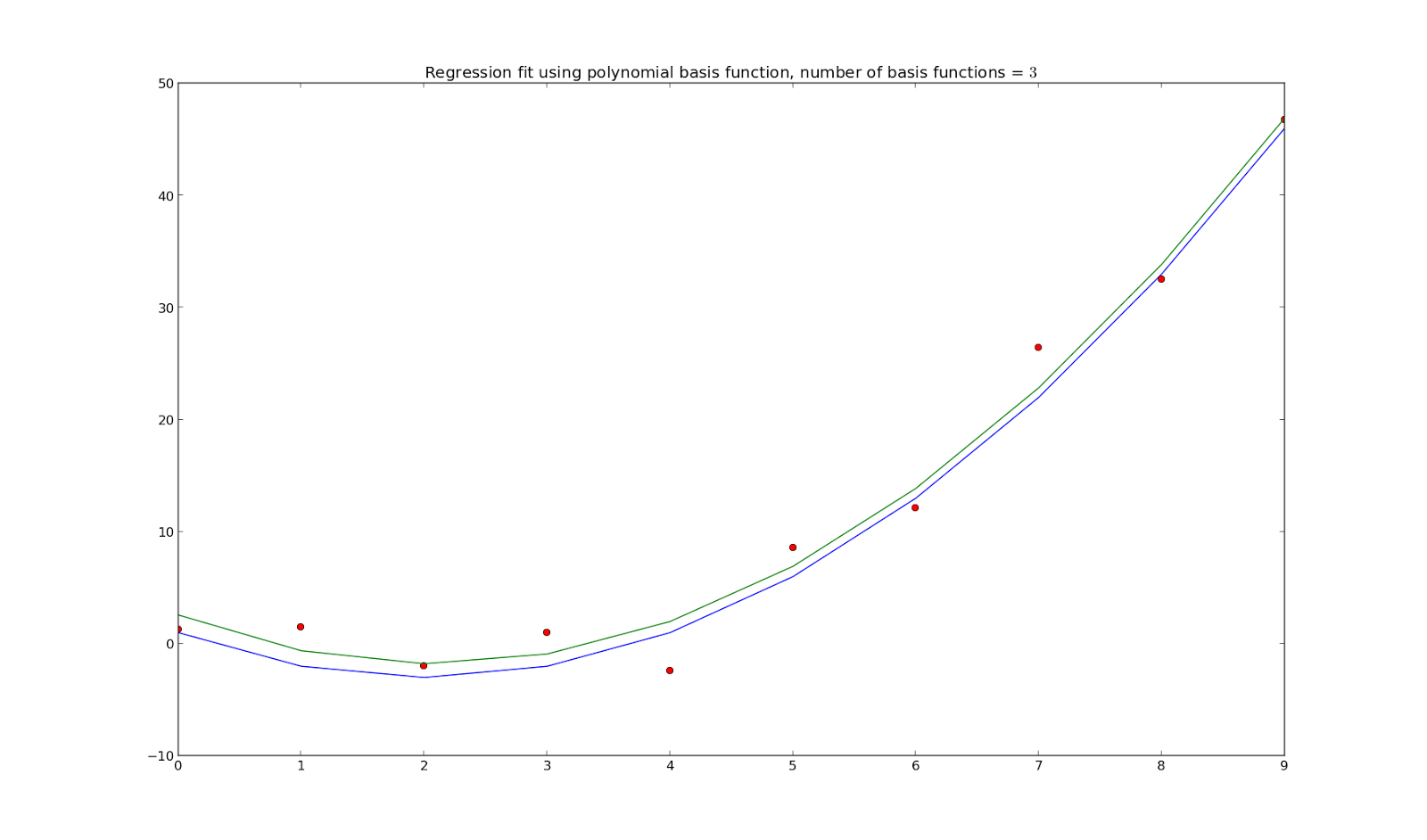
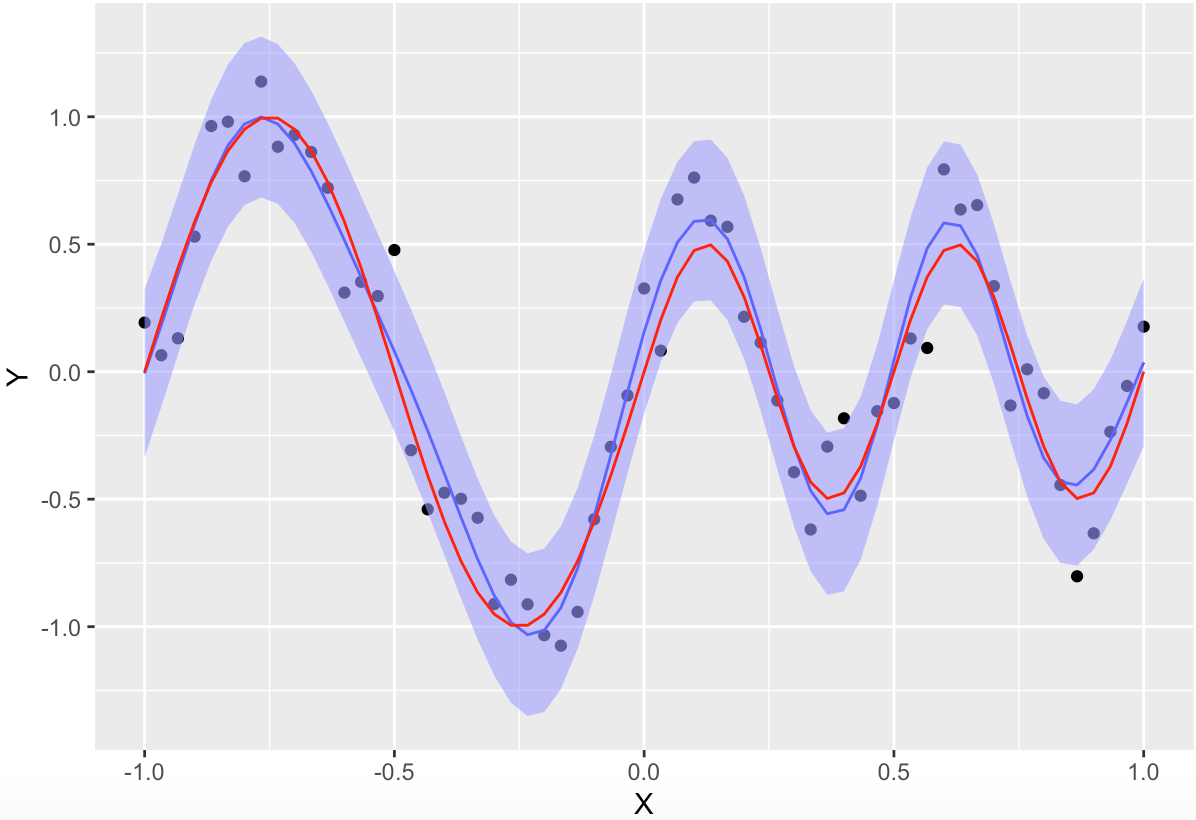
Bayesian linear regression:
On the same sheet of paper, I just have a belief of all possible rulers that can fit those dots. No single ruler is actually placed. Rulers here can have a variety of shapes, and can be assembled together (analogous to basis functions applied to input features). The rulers may be rugged, so whenever you draw some lines with the rulers (analogous to evaluating the model), you get slightly different lines each time (to denote uncertainty or noise inherent to the parameters of the model)
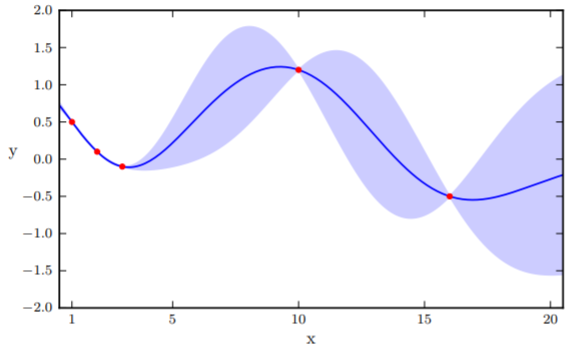
Gaussian process:
On the same sheet of paper with dots, I only hold the belief of what are all the plausible lines that can go through the dots. The absence of a ruler is to denote that a GP is typically non-parametric and models the function space directly. The analogy to the prior belief here is that before even given the paper, I have some sort of intuition as to what lines are plausible, with the constraint that I have to believe in lines (this is mathematically expressed by the Kernel which isn’t a diagonal matrix, therefore points of the lines are not independent to one another). As I observe datapoints during training, I can both guide the trajectory of the lines, and ignore prior lines which clearly don’t fit the dots.
Recommended Reading
For the technical details behind linear regression, with and without the Bayesian treatment, along with Gaussian Processes, I recommend reading either of these freely available textbooks:
- Murphy, Kevin P. (2022) Probabilistic Machine Learning: An Introduction. https://probml.github.io/pml-book/book1.html
- Bishop, Christopher (2006) Pattern Recognition and Machine Learning. https://www.microsoft.com/en-us/research/publication/pattern-recognition-machine-learning/
P.S.: To me, Murphy’s book is more recent, but discusses topics in a more straightforward manner. Murphy also has available code to run. Bishop goes into a bit more detail, but his notation is a bit outdated.
Enjoy Reading This Article?
Here are some more articles you might like to read next: